Sag’s mit einer Blume, und Dein Ansinnen wird freundlicher aufgenommen.
Das tat ich spontan mit einem feature request an den Autor von pgfplots. Nun weiß ich, dass er generell gern auf Fragen antwortet und Neues implementiert und das Paket sehr gut pflegt. Umso mehr Grund für ein Blümchen. 🙂
Wenn ich Funktionen mit Polarkoordinaten parametrisiere, insbesondere mit Rotations-Symmetrie, habe ich oft mit Winkelfunktionen zu tun, also mit den trigonometrischen Funktionen wie beispielsweise Sinus und Cosinus. Winkel kann man in Grad angeben, den Vollkreis von 0 bis 360 Grad durchlaufen, oder man verwendet Radiant, entsprechend von 0 bis 2*pi. pgfplots verwendet Grad. Wenn ich das weiß, gebe ich den Quellbereich eben in Grad an und gut ist es, wie in dieser ersten Blüte:

Der Code hierfür ist:
\usepackage{pgfplots}
\pgfplotsset{compat=1.8}
\renewcommand*{\r}{(sin(4*u)^3 + cos(2*u)^3 + sin(6*v)^2 + cos(6*v)^4)}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
view = {120}{310},
hide axis,
colormap = {flower}{
color(0cm) = (yellow); color(4cm) = (yellow!70!red);
color(8cm) = (red!60!black); color(12cm) = (red!90!black);
color(16cm) = (green); color(20cm) = (green!20!black)},
]
\addplot3[
surf,
z buffer = sort, point meta = u,
domain = 0:180, domain y = 0:360,
samples = 80, samples y = 80,
variable = \u, variable y = \v
]
( { \r*sin(u)*cos(v) },
{ \r*cos(u) },
{ \r*sin(u)*sin(v) } );
\end{axis}
\end{tikzpicture}
\end{document}</pre>
Ich lasse die Parameter u und v also einfach in Grad laufen. Doch was, wenn es komplizierter wird? pgfplots bietet an, mit deg() umzurechnen, also etwa sin(deg(x)) zu schreiben. Wenn ich jedoch neben trigonometrischen auch hyperbolische Funktionen verwende, zum Beispiel sinh (sinus hyperbolicus) und cosh (cosinus hyperbolicus), die nicht Grad verwenden, komme ich in diesem Mix leicht durcheinander. Und ich kann ja auch mal komplett nur in Radiant rechnen wollen.
Bei dieser zweiten Blüte kann man die Schwierigkeit des wiederholten Umwandelns leicht sehen:
\usepackage{pgfplots}
\pgfplotsset{compat=1.8}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
view = {60}{-60},
hide axis,
colormap = {flower}{%
color(0cm) = (yellow); color(4cm) = (orange);
color(8cm) = (red!40!black); color(12cm) = (red!80!black);
color(16cm) = (green); color(20cm) = (green!20!black)},
]
\addplot3[
surf,
z buffer = sort, point meta = u,
domain = -13.2:13.2, domain y = -37.4:37.4,
samples = 80, samples y = 120,
variable = \u, variable y = \v
]
( { -u + (2*0.84*cosh(0.4*u)*sinh(0.4*u))/(0.4*((sqrt(0.84)*cosh(0.4*u))^2
+ (0.4*sin(deg(sqrt(0.84)*v)))^2)) },
{ (2*sqrt(0.84)*cosh(0.4*u)*(-(sqrt(0.84)*sin(deg(v))
* cos(deg(sqrt(0.84)*v))) + cos(deg(v))*sin(deg(sqrt(0.84)*v))))/(0.4
* ((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(deg(sqrt(0.84)*v)))^2)) },
{ (2*sqrt(0.84)*cosh(0.4*u)*(-(sqrt(0.84)*cos(deg(v))
* cos(deg(sqrt(0.84)*v))) – sin(deg(v))*sin(deg(sqrt(0.84)*v))))/(0.4
* ((sqrt(0.84)*cosh(0.4*u))^2 + (0.4*sin(deg(sqrt(0.84)*v)))^2)) });
\end{axis}
\end{tikzpicture}
\end{document}</pre>
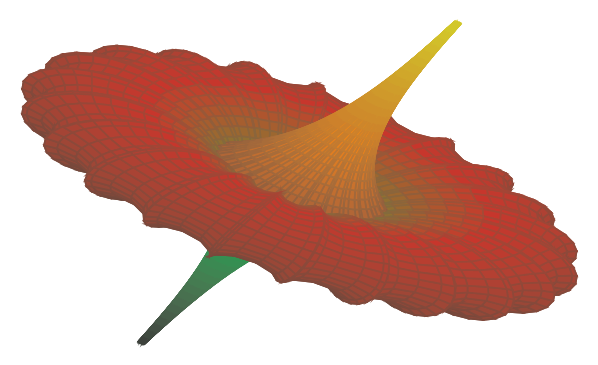
Wenn man jetzt einen Trick hätte, die interne Rechnung auf Radiant umzustellen, oder pgfplots das als Einstellung unterstützen würde, wäre die Formel einfacher aufzuschreiben und zu lesen.
Nachdem ich das auf TeXwelt mitteilte und diesen kleinen Blumenstrauß symbolisch mit überreichte, antwortete Christian Feuersänger, der Autor des pgfplots-Pakets, dass die kommende Version 1.11 mit einem global konfigurierbarem Format fuer trigonometrische Funktionen kommt. Dann schreibt man \pgfplotsset{trig format plots=rad} in die Präambel und es werden alle plot-Ausdrücke automatisch in Radiant gerechnet.
Ich bedanke mich sehr für die Reaktion und die Implementierung dieses Features.
Die von mir so eingefärbten “Blumen” sind natürlich als mathematische Funktionen seriöse Forschungs-Objekte, die erste ist die Oberfläche einer Kugelflächenfunktion (Spherical Harmonic Surface), die zweite ist eine parametrische pseudosphärische Blasebalg-Oberfläche. Auf Englisch klingt auch sie als Parametric Breather Pseudospherical Surface besser. 🙂 Mehr darüber sowie zur Technik und einen Vorschlag von Elke kann man im originalen Beitrag auf TeXwelt lesen: Kann man bei pgfplots die Argumente trigonometrischer Funktionen von Grad auf Radiant umstellen?