
Neulich hatte ich sie mal wieder in den Fingern: das klassische Beispiel für eine periodische Funktion, die Sinus-Funktion. Kennt jeder, die horizontale “Welle” im kartesischen Koordinatensystem. Ausgehend von einer polaren Darstellung und einer komplexeren Sinus-Funktion werde ich hier im Folgenden einen räumlichen Blick auf eine eigentlich zweidimensionale Funktion werfen.
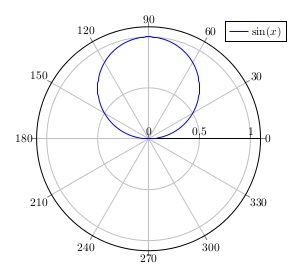
Im Polarkoordinatensystem vereinfacht sich die Darstellung: es ist ein simpler Kreis, der mit steigendem (fallendem) Winkel immer wieder durchlaufen wird. Der Vollkreis entspricht ja genau der Periodenlänge.
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{polar}
\begin{document}
\begin{tikzpicture}
\begin{polaraxis}[
domain = 0:180,
samples = 100,
]
\addplot[thick, blue] {sin(x)};
\legend{$\sin(x)$}
\end{polaraxis}
\end{tikzpicture}
\end{document}
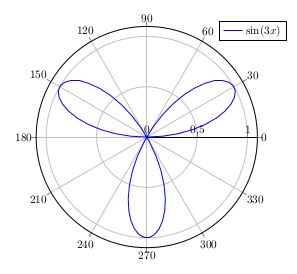
Wenn wir die Periodenlänge verkürzen, erhalten wir:
Wir können das natürlich ziemlich weit treiben – statt eines riesigen Faktors kann man auch einen gebrochenen Faktor nehmen, der nicht gerade ein großer Teiler eines kleinen Vielfachen von 360 Grad ist. Man kann schon nette Bildchen erhalten, denen man den Sinus nicht mehr direkt ansieht.
\documentclass{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{polar,colormaps}
\begin{document}
\begin{tikzpicture}
\begin{polaraxis}[
domain = -14400:14400,
samples = 3000,
colormap/cool,
hide axis
]
\addplot[no markers,mesh,opacity=0.5] {1-sin(40*x/39};
\end{polaraxis}
\end{tikzpicture}
\end{document}

Wenn wir noch einen Sinus mit anderen Faktoren addieren, haben wir mehr Bewegung – diesen Plot hatte ich neulich auf TeXwelt:
\documentclass{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{polar}
\begin{document}
\begin{tikzpicture}
\begin{polaraxis}[
domain = -3600:3600,
samples = 4000
]
\addplot[blue!50!black] {1 - sin(50*x/49) - sin(8*x)};
\end{polaraxis}
\end{tikzpicture}
\end{document}
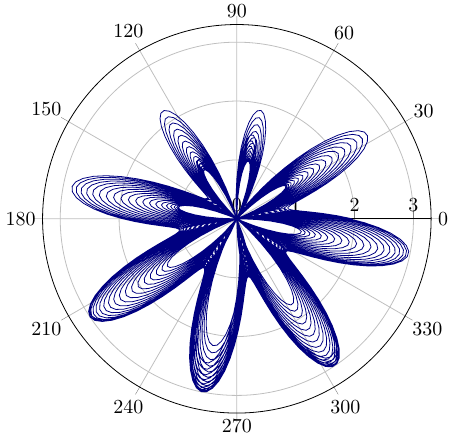
Den tatsächlichen Verlauf kann man noch nicht so gut erkennen. Jetzt könnte man vielleicht einfärben, je nach Umdrehung, also nach Winkel. Oder man hebt es in die dritte Dimension, mit wachsendem Winkel nach oben, darum ging es mir bei diesem Beispiel auf TeXwelt. Das würde auch einen guten Blick auf die Funktion verschaffen.
Wir erstellen einen parametrischen 3d-Plot in x und y: x durchläuft nur einmal den Vollkreis von -180 bis 180 Grad, weiterhin geben wir auch ein sampling für y vor, was für die Anzahl der Umdrehungen steht. Dem Funktions-Argument wird y mal 360 Grad addiert. y dient uns als dritte Dimension, während x als Winkel sowie der Funktionswert die ursprünglichen zwei Dimensionen sind. Nähere Erklärung: hier auf TeXwelt.
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
domain = -180:180,
y domain = -19:19,
samples y = 39,
samples = 100,
z buffer = sort,
colormap/cool,
grid
]
\addplot3[data cs = polar, surf]
( {x}, {1 - sin(50*(x+360*y)/49) - sin(8*(x+360*y))}, {y} );
\end{axis}
\end{tikzpicture}
\end{document}
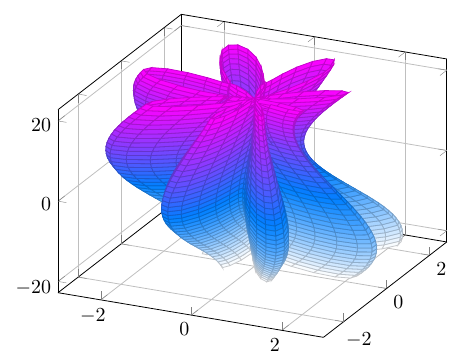
Und hier haben wir den eigentlichen Anlass für diesen Blog-Post – einmal zu erzählen, wie man eine komplizierter werdende Funktion sowohl polar als auch in drei Dimensionen darstellen kann.