Gerade habe ich mich mit Tschebyschow-Polynomen beschäftigt. Das sind spezielle orthogonale Polynome, die in Mathematik und Physik für die Lösung gewisser Differentialgleichungen nützlich sind. Trockene Mathematik braucht hier nicht zu sein, ich möchte nur einmal gewonnene schöne Darstellungen zeigen.
Die Serie der Polynome ist:
 T0(x) = 1 T1(x) = x
T0(x) = 1 T1(x) = x
T2(x) = 2x2 – 1 T3(x) = 4x3 – 3x
T4(x) = 8x4 – 8x2 + 1
T5(x) = 16x5 – 20x3 + 5x
T6(x) = 32x6 – 48x4 + 18x2 – 1
T7(x) = 64x7 − 112x5 + 56x3 − 7x
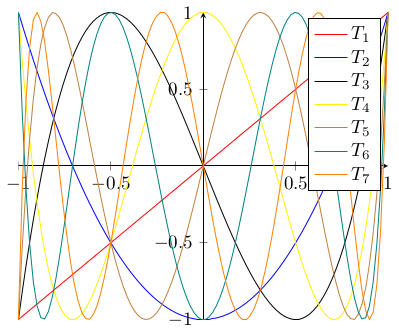
Soweit, so unverdächtig. Schauen wir uns nun verschiedene Darstellungsmöglichkeiten an.
Man kann ein Entwicklungsgesetz erkennen: Tn(x) = 2xTn-1(x) – Tn-2(x). Ehe ich 20 und mehr Polynome eintippe, wie ich später brauchen werde, könnte ich das ja rekursiv definieren. Doch in dem Fall nutze ich noch eine Eigenschaft aus, nämlich: Tn(cos(x)) = cos(nx). Auf mathematische Beweise verzichte ich, wie eingangs angedeutet. Letzteres stelle ich um und plotte in einer for-Schleife:
\documentclass{standalone}
\usepackage{pgfplots}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
axis lines = middle,
cycle list name = color list,
legend entries = { $T_1$, $T_2$, $T_3$, $T_4$,
$T_5$, $T_6$, $T_7$ }
]
\foreach \n in {1, ..., 7}
\addplot+[domain=-1:1, samples=100]
{ cos(\n*acos(x)) };
\end{axis}
\end{tikzpicture}
\end{document}
Auf Wolfram Mathworld fand ich dann eine interessante Darstellung:

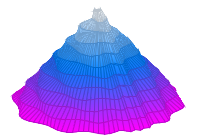
Das wollte ich gleich nachvollziehen, nur weil es hübsch ist, auch wenn man die einzelnen Kurven nicht mehr wirklich unterscheiden kann. Dazu steht dort geschrieben: “A beautiful plot can be obtained by plotting Tn(x) radially, increasing the radius for each value of n, and filling in the areas between the curves.”
Ok, wir plotten polar mit wachsendem Radius und füllen die Zwischenräume. Ich habe echt eine Weile überlegt, wie die Erzeugungsvorschrift konkret ist, und kam dazu:
- wie oben die Funktion Radius = cos(n arccos(Winkel) nehmen,
- den Definitionsbereich -1 … 1 auf den Vollkreis strecken (360 Grad),
- nochmal spiegeln, also negativen Radius nehmen,
- nur die geraden Polynome nehmen,
- schlicht zu jedem Tn den Wert n addieren,
- die samples je nach n für bessere Darstellung erhöhen,
- zwischen aufeinanderfolgenden Funktionen abwechselnd füllen und nicht füllen.
Als LaTeX-Dokument für den Plot verfasste ich dann:
\documentclass{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{polar,fillbetween}
\newcommand*{\maximum}{26}
\begin{document}
\begin{tikzpicture}
\begin{polaraxis}[hide axis]
\pgfplotsinvokeforeach{0,...,\maximum}{
\pgfmathparse{20+#1^2}
\pgfplotsset{samples=\pgfmathresult}
\addplot[name path = #1, mark=none, solid, domain=0:360]
{ -(#1*2 + cos(#1*2*acos(x/180-1))) }; }
\addplot[name path=-1] coordinates {(0,0)};% Startbezug filling
\foreach \i [evaluate=\i as \j using int(\i-1)] in {0,2,...,\maximum}{
\edef\temp{[black] fill between[of=\i\space and \j]}
\expandafter\addplot\temp;
}
\end{polaraxis}
\end{tikzpicture}
\end{document}
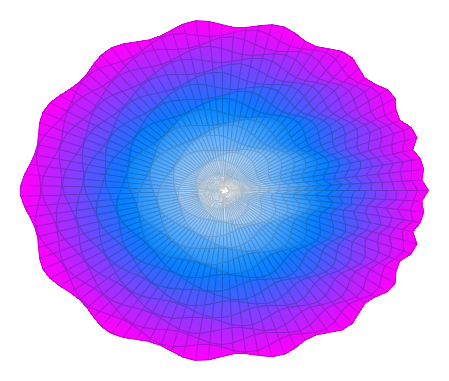
Die Ausgabe:

Eine Sache fällt auf: ich habe nicht einfach \foreach verwendet. Hierbei kommt es nämlich leicht zu Problemen, da \foreach nicht sofort sein Argument expandiert. \pgfplotsinvokeforeach hingegen wertet aus. Eine weitere Möglichkeit ist, die Ausdrücke mit enthaltenen Schleifenvariablen erst zu expandieren, und dann an \addplot zu übergeben. Ein winziger nötiger Trick war hier noch, ein beim Expandieren verschlucktes Leerzeichen explizit einzufügen durch \space. Erklärt hatte ich das auch hier auf der TeXwelt: Wie kann man mit pgfplots Pfade in einer Schleife verwenden? So kann ich jedenfalls die Variable im Pfadnamen ohne Fehlermeldung innerhalb von Schleifen verwenden.
Wir können uns auch eine Schleife sparen. Ich erzeuge hier einen einzigen 3d-Plot, nehme das n in die dritte Dimension. Wenn ich senkrecht draufschaue durch view = {0}{90}, habe ich wieder einen 2d-Plot. Ich brauche nur einen Plot-Aufruf mit ein paar settings fürs Aussehen, das unnötige Negieren auch weggelassen:
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{colormaps}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
data cs = polar,
hide axis,
colormap/cool,
point meta = -z,
view = {0}{90}
]
\addplot3[surf, shader=faceted interp, domain=0:360, samples=100,
y domain = 0:20, samples y = 20, z buffer = sort]
( {x}, { y*2 + cos(y*2*acos(x/180-1))}, {20-y} );
\end{axis}
\end{tikzpicture}
\end{document}
Und da zig sich schneidende Funktionen auf der Ebene nicht optimal darstellbar sind, heben wir es hoch und betrachten es in der dritten Dimension – die Spitze sagt genug aus, es wiederholt sich ja nur:
\documentclass{standalone}
\usepackage{pgfplots}
\usepgfplotslibrary{colormaps}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
data cs = polar,
grid,
colormap/cool,
point meta = -z,
view = {60}{30} ]
\addplot3[surf, shader = faceted interp, domain = 0:360,
samples=100, y domain = 0:11, samples y = 12, z buffer = sort]
( {x}, { y*2 + cos(y*2*acos(x/180-1))}, {20-y} );
\end{axis}
\end{tikzpicture}
\end{document}
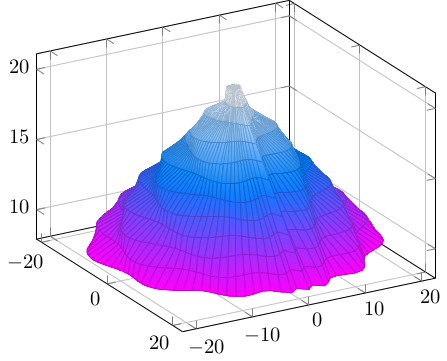
Was dem Schwarzweiß-Muster zugrundeliegt, können wir hier nun besser sehen. Das Paket pgfplots als vielseitiges 2d- und 3d-Plot-Programm vereinfacht uns hier die Arbeit.