Nachdem ich im vorangehenden Post erwähnte, dass ich auch pgfplots zur grafischen Ausgabe nutze, möchte ich hier ein paar Beispiele nennen.
Als Vorteile von pgfplots gegenüber Basis-TikZ nutze ich hier:
- einfaches Plotten mit 3D-Koordinaten und Schrägbildansicht
- Darstellung zugehöriger Koordinatenachsen
- Verwenden von Farbverläufen
- Einlesen von Dateien, falls die Daten extern berechnet wurden.
In jedem Fall kann man hier wieder Lua zum Berechnen der Daten verwenden. Lua generiert uns die TeX-Befehle zur Ausgabe, die in der pgfplots-Achsen-Umgebung verarbeitet werden.
Hier die Beispiele, einfach draufklicken, um zur zugehörigen Diskussion auf TeXwelt zu gelangen, wo man den vollständigen Quellcode findet.
Lorenz-Attraktor (Dynamisches System)
Während ich auf TeXwelt eine auf Python basierende Version postete, brachte Henri eines, was LuaTeX verwendet, daher zunächst sein Bild:
Von pgfplots nutzte ich neben der einfachen 3D-Darstellung die Fähigkeit zum durchscheinenden Plotten, so erhalte ich eine Dichte-Darstellung:
Und der Code, hat man einmal die Daten berechnen lassen, ist einfach:
\documentclass[border=10pt]{standalone}
\usepackage{pgfplots}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
xmin = -25, xmax = 25,
ymin = -25, ymax = 25,
zmin = 0, zmax = 50,
hide axis,
]
\addplot3[mark=none, mesh, shader=interp, color=black, opacity=0.2]
file { lorenz.dat };
\end{axis}
\end{tikzpicture}
\end{document}
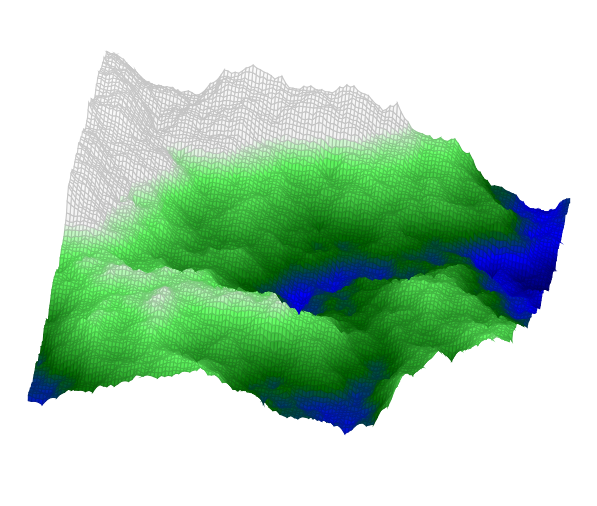
Fraktale Landschaften (Grundansatz für Produktion prozeduraler Welten)
Zwischen benachbart liegenden Punkten werden neue Punkte bestimmt mit zufälligen, aber begrenzten Variationen, was am Ende eine bergige “Landschaft” ergibt. Die errechneten Punkte gebe ich mit Farben entsprechend ihrer Höhe aus, also blau für Meeresspiegelhöhe und darunter, grün für Berge und weiß ab “Schneegrenze”.
Nächster Schritt: ein paar Startwerte vorgeben, um mit einer vordesignten Grobstruktur zu starten, wie etwa einer Insel im Wasser.
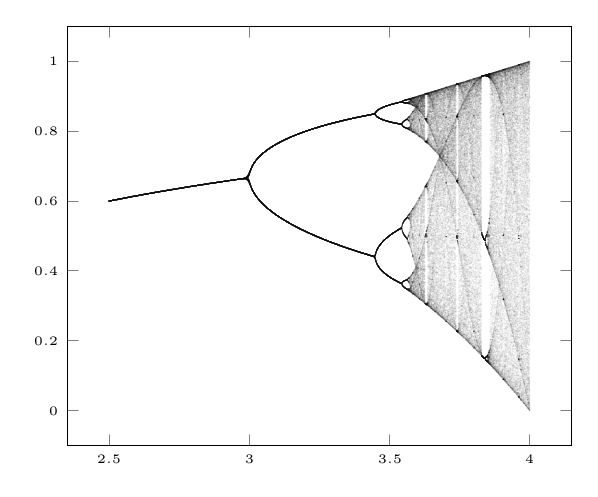
Feigenbaum-Diagram (Bifurkationen)
Ein Klassiker der Chaos-Theorie und eng verwandt mit der Mandelbrot-Menge. Auch hier wird Transparenz verwendet für einen Eindruck der Punktdichte.
Themen dieser Art schneide ich auf TeXwelt.de gern an. Dort fragen nicht nur Bachelor-Schreiber um Hilfe, sondern es hat sich auch eingebürgert, dass TeX-Kenner und TikZ-Freunde ihre Ideen als Fragen in den Raum stellen und oft selbst eine der Antworten dazu geben.