Heute habe ich einen Plot überarbeitet, um ihn auf TeXnique.fr zu stellen. Also, der sollte ungefähr so aussehen:

(Foto von Guido Draheim).
Also wie ein Spritzkuchen, auch Spritzring genannt. Nur, hm, mathematischer und digitaler.
Wie zeichnet man das?
Erstmal einen Querschnitt überlegen. In Polarkoordinaten ergibt die Sinus-Funktion sin(x) einen Kreis, sin(3x) sind drei Blätter, wir geben noch ein bisschen Radius (1,25) als Mittelstück. Das ergibt die Funktion sin(3x) + 1.25 in Polarkoordinaten:
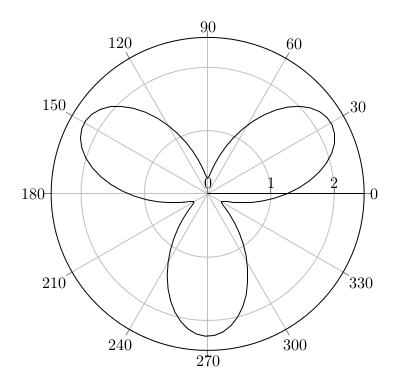
Den betten wir in den Raum ein, etwa in der xy-Ebene mit z=0 als (x,y,z)(t) = ( cos(t)(sin(3t)+1.25), sin(t)(sin(3t) + 1.25), 0 ):
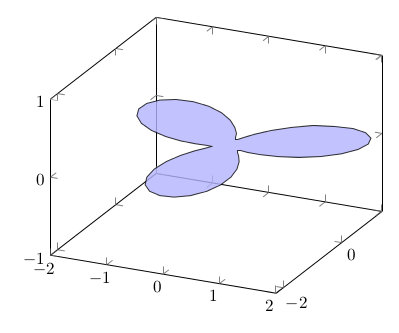
Oder anders gedreht:

Wir können geradeaus im Raum schieben, wenn wir beispielsweise in der xz-Ebene zeichnen und mit linearem y verschieben: (x,y,z)(t) = ( cos(t)(sin(3t)+1.25), t, sin(t)(sin(3t)+1.25) ). Das sieht im Raum dann so aus:
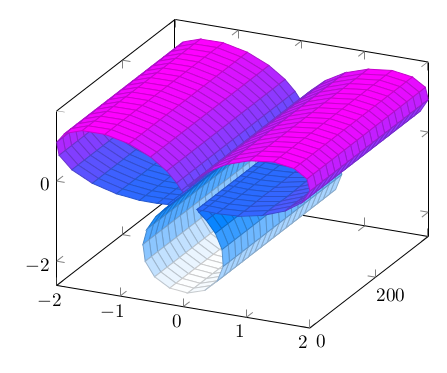
Doch wir wollen ja drehen. Im Raum im Kreis gedreht, verwenden wir eine Torus-Abbildung, etwa:
x(t,s) = (2+cos(t))cos(s+pi/2)
y(t,s) = (2+cos(t))sin(s+pi/2)
z(t,s) = sin(t)
Und das verknüpfen wir wir mit unserer Funktion:
x(t,s) = (6+(sin(3t)+1.25)cos(t))cos(s)
y(t,s) = (6+(sin(3t)+1.25)cos(t))sin(s)
z(t,s) = (sin(3t)+1.25)sin(t)
Hier ein Schnitt davon, nur im Halbkreis rotiert:

Hier das gesamte Torus-basiert gedrehte Bild der Ursprungsfunktion:

Und nun der Twist. Wir können das Ganze noch verdrehen, indem wir im Funktions-Argument ein Vielfaches von t bzw. y addieren und durch mit wachsendem y eine Drehung erreichen:

Mathematik ist erledigt, jetzt noch bisschen Farbe und Schick dazu. Ok, jetzt endlich mal Code:
% !TEX lualatex
% Mit LuaLaTeX übersetzen, weil die Berechnungen zu aufwendig für pdfLaTeX sind
\documentclass{standalone}
\usepackage{pgfplots}
\usetikzlibrary{backgrounds}
\begin{document}
\begin{tikzpicture}
\begin{axis}[axis equal,
hide axis,
/tikz/background rectangle/.style = {
left color = black,
right color = black!20,
shading angle = 135,
},
show background rectangle
]
\addplot3[
surf,
shader = flat,
miter limit = 1,
domain = 0:360,
y domain = 0:360,
samples = 100,
samples y = 70,
z buffer = sort,
colormap/hot2,
]
( {(6+(sin(3*(x+3*y))+1.25)*cos(x))*cos(y)},
{(6+(sin(3*(x+3*y))+1.25)*cos(x))*sin(y)},
{((sin(3*(x+3*y))+1.25)*sin(x))} );
\end{axis}
\end{tikzpicture}
\end{document}
Und das ergibt:

Alle Codes und weitere Erklärungen sind hier:
- Deutsch: Drehtransformation mit pgfplots, mein ursprünglicher Post auf TeXwelt.de
- Englisch: Rotation transformation of a parametrized plot, mit Antwort von cmhughes auf TeX.SE
- Französisch: Représenter un vissage à l’aide de pgfplots, heute geschriebene und erweiterte Version in französisch verfasst auf TeXnique.fr