Wenn Funktionswerte zu groß werden, können wir die grafische Darstellung beschneiden. Wie machen wir es geschickt, damit es auch noch gut aussieht? Wenn wir beispielsweise einen Surface-Plot zeichnen, die Oberfläche der Funktion durch sogenannte Patches darstellen, kann es etwas gezackt aussehen, statt gerade. Wie schlimm, richtet sich nach Anzahl der Samples, also der Teilpunkte: wählen wir mehr, so wird es feiner.
Schauen wir es uns am Beispiel an. Wir plotten einen Kegel und beschränken den Maximalwert der Höhe durch die Option restrict z to domain:
\usepackage{pgfplots}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
grid,
domain=-5:5, y domain=-5:5,
xmin=-10, xmax=10,
ymin=-10, ymax=10,
zmin=0,
restrict z to domain=0:5]
\addplot3 [surf] {sqrt(x^2 + y^2};
\end{axis}
\end{tikzpicture}
\end{document}</pre>
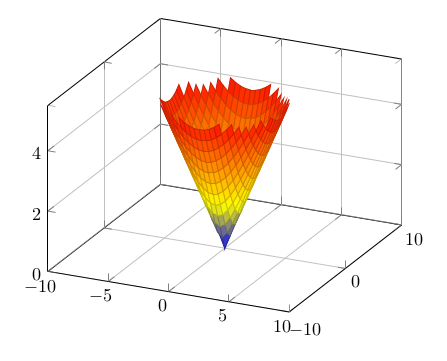
Ziemlich ausgefranst. Wir können anders beschneiden durch eine Variante der genannten Option mit *, also restrict z to domain*=0:5, das wird glatter:
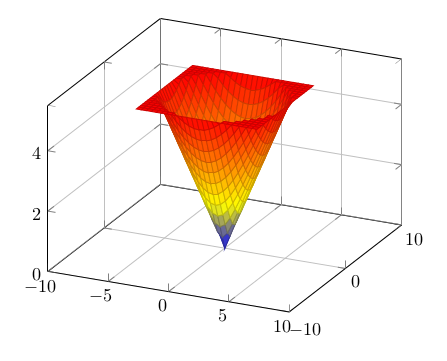
Doch das sieht nicht mehr genau nach dem Kegel aus.
Statt kartesisch in x und y zu sampeln und den Funktionswert direkt zu plotten, können wir die Funktion parametrisieren. Clevererweise stellen wir gleich so um, dass wir die Höhe als Laufvariable haben, also von vornherein Niveauflächen haben, wo Beschneidung parallel zur xy-Ebene einfach einen glatte Kante ergeben muss.
Erinnert man sich an Polarkoordinaten, fällt eine Umstellung ins Auge: obiger z-Wert wäre der Abstand r zum Nullpunkt, dann wissen wir noch die Formeln x=r*cos(phi) und y=r*sin(phi) oder betrachten das rechtwinklige Dreieck. Jedenfalls parametrisieren wir in r und dem Winkel phi. Machen uns nicht die Mühe, neue Variablen einzuführen und nennen das wieder x und y, erhalten wir diese Parameterdarstellung:
\usepackage{pgfplots}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
grid,
domain=0:5, y domain=0:360,
xmin=-10, xmax=10,
ymin=-10, ymax=10,
zmin=0,
]
\addplot3 [surf] ( {x*cos(y)}, {x*sin(y)}, {x} );
\end{axis}
\end{tikzpicture}
\end{document}</pre>
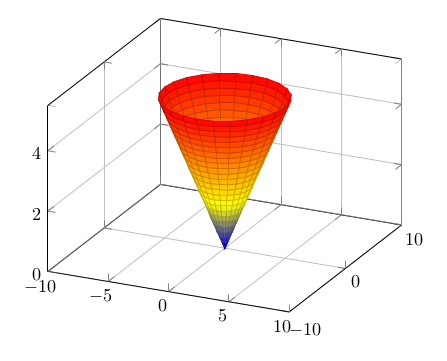
Das ist nun wirklich gut. Die neue radiale Parametrisierung erkennt man auch an den Isolinien.
Bisschen einfaches Beispiel, oder? Dennoch kann man das (Um-)Parametrisieren anwenden, auch wenn es mal komplizierter wird.
Nehmen wir eine neue Herausforderung an? Plotten wir z = x*y/(x^2+y^2)^2:
\usepackage{pgfplots}
\usepgfplotslibrary{colormaps}
\begin{document}
\begin{tikzpicture}
\begin{axis}[
restrict z to domain = -12:12,
colormap/autumn,
view/el = 45
]
\addplot3[
surf,
samples = 70,
domain = -0.5:0.5,
domain y = -0.5:0.5,
]
{x*y/(x^2+y^2)^2};
\end{axis}
\end{tikzpicture}
\end{document}</pre>
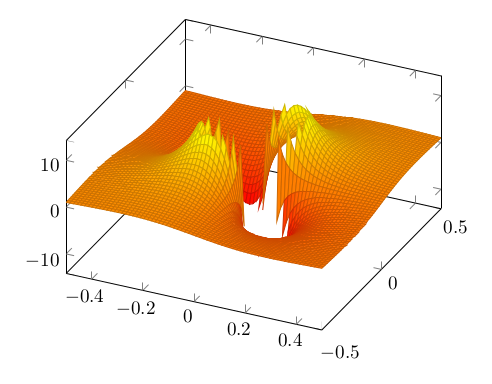
Das Problem ist wieder erkennbar. Diesmal wird es mit restrict z to domain* besser:
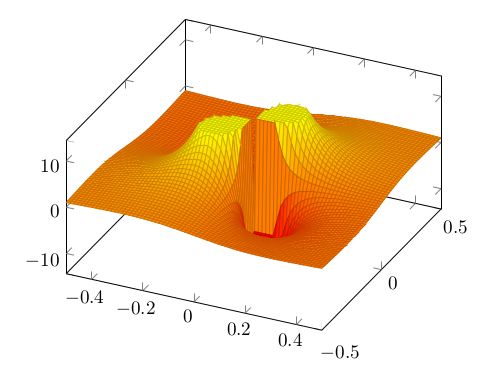
Es steht nichts über. Eigentlich ok. Die Eckigkeit ist halt nicht mehr vertikal, sondern horizontal, immer noch angeknabbert (neuer Fachausdruck dafür).
Parametrisieren in z? Freiwillige vor! I’m afraid we need to use…MATH!
Das könnte hier bisschen schwierig werden, auch wenn es wieder schön symmetrisch in x und y aussieht. Machen wir es diesmal anders. Nutzen wir unsere Tools. Nachdem ich diese Frage auf TeXwelt.de in den Raum stellte: Wie erhalte ich einen glatten Rand bei beschränkten Plots? und Vorschläge in den Raum stellte, gab Christian Feuersänger, der Autor von pgfplots, eine Lösung durch einen Kontur-Plot an. Im Hintergrund wird gnuplot aufgerufen, write18 (shell-escape) sollte daher aktiviert sein.
Diese beiden Plots kommen hinzu (voller Code auf TeXwelt):
\addplot3[
contour gnuplot={
levels={12},
labels=false,
},
samples = 70,
domain = -0.5:0.5,
domain y = -0.5:0.5,
]
{x*y/(x^2+y^2)^2};
% Konturlinie füllen, myfile_contourtmp0.table ist die
% oben nebenbei generierte Datei zu myfile.tex:
\addplot3[
% 1000 ist immer der letzte Eintrag der colormap
% also point meta max:
/utils/exec={\pgfplotscolormapdefinemappedcolor{1000}},
draw=none,
fill=mapped color]
file {myfile_contourtmp0.table};</pre>
So erhalten wir einen ordentlichen Plot:
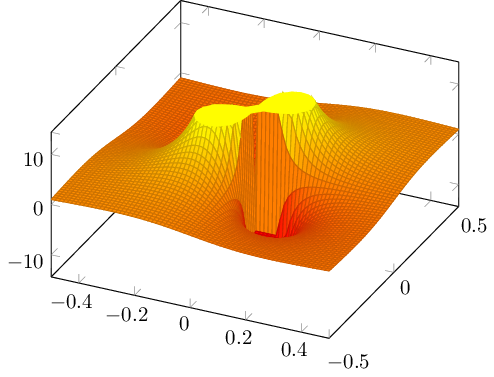
Damit haben wir eine weitere Möglichkeit, die Schnittstellen einer Funktion gezielt nachzuzeichnen oder mit Farbe zu füllen.